Dolanma düzlemi nedir? Fizikteki rolü nelerdir?
Dolanma düzlemi, özellikle kuantum fiziği ve astronomi gibi alanlarda büyük öneme sahiptir. Peki, dolanma düzlemi nedir? Fizikte dolanma düzleminin önemi nedir? İşte konunun tüm ayrıntıları...
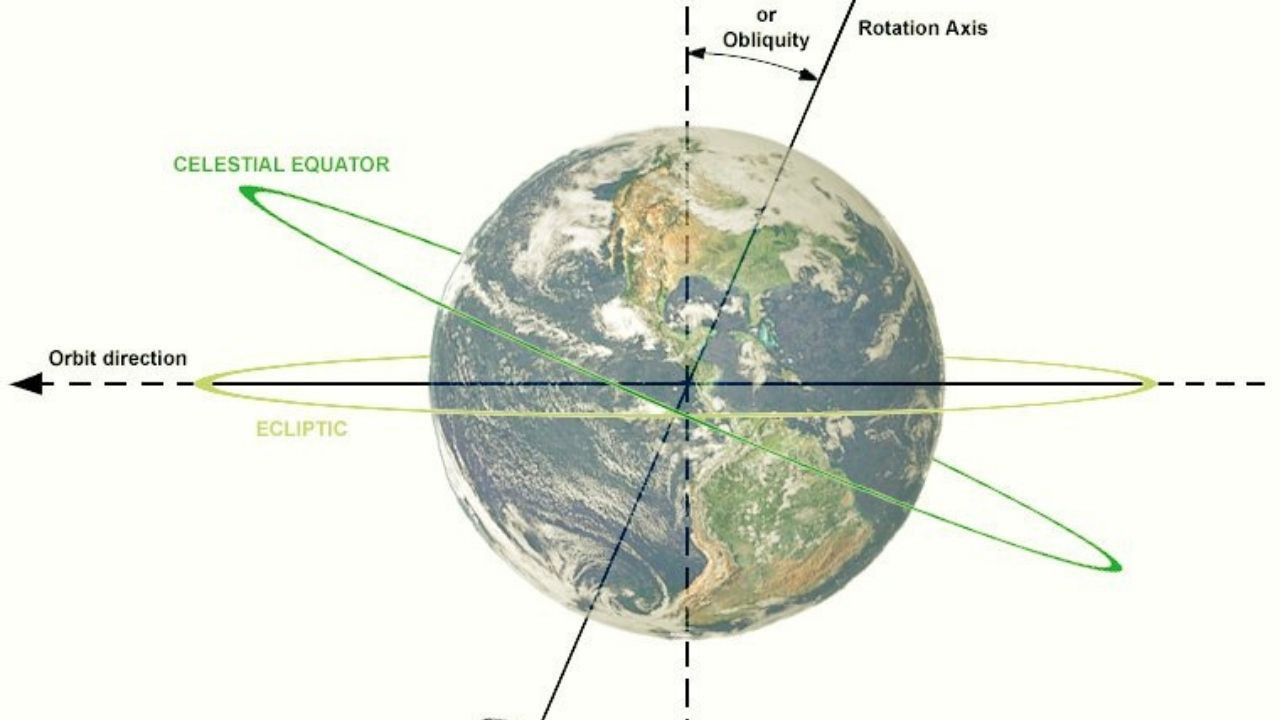
Dolanma düzlemi, fiziğin önemli kavramlarından biridir ve iki nesnenin birbirine dolanık olduğu anlarda ortaya çıkan düzlemi ifade eder. Dolanma düzlemi hesaplamaları, genellikle geometrik analiz yöntemleri kullanılarak gerçekleştirilir. Bu yöntemler, düzlemin konumunu ve dolanma derecesini belirlemede kritik rol oynar. Dolanma düzlemi analizleri, bilim insanlarına maddenin ve enerjinin karmaşık yapısını daha iyi anlama fırsatı sağlar.
DOLANMA DÜZLEMİ NEDİR?
Dolanma düzlemi, fizik ve mühendislik alanında sıkça kullanılan bir terimdir. Tüm uzay geometrisi kuralları içinde, bir cismin dönme veya dolanma hareketini analiz ederken kritik bir rol oynar. Özellikle hareketli cisimlerin eksenel hareketlerini açıklamak için kullanılır. Bu nedenle, dolanma düzleminin doğru bir şekilde anlaşılması, karmaşık sistemlerin daha etkili bir şekilde modellenmesine katkı sağlar.
Fizikteki bu kavram, hem teorik hem de pratik uygulamalarda yaygın olarak kullanılmaktadır. Dolanma düzleminin temel özelliklerini anlamak, bu alanlarda yapılan çalışmalarda derinlemesine bir anlayış sağlamak için önemlidir. Aşağıda, dolanma düzlemi ile ilgili bazı temel unsurları sıraladık:
Dolanma Düzlemi ile İlgili Temel Unsurlar
- Rotasyon ekseni
- İnertial referans noktası
- Düzlem simetrisi
- Açısal momentum
- Enerji dönüşümü
- Vektör analizi
- Dönüşüm matrisleri
Bu unsurlar, dolanma düzleminin anlaşılmasında kritik öneme sahiptir. Dolanma düzlemindeki her bir eleman, fiziksel sistemlerin hareketlerini daha iyi modellemek ve analiz etmek için kullanılır. Modern mühendislik çözümleri, bu düzlemin inceliklerini anlamadan tam olarak etkili olamaz.
DOLANMA DÜZLEMİNİN FİZİKTEKİ ROLÜ
Dolanma düzleminin fizikteki rolü, özellikle mekanik sistemlerde, dönme hareketlerinin daha iyi anlaşılmasına yardımcı olmaktır. Düzlemin belirli bir sisteme nasıl uygulandığı, sistemin kararlığı ve dinamikleri üzerinde doğrudan etkiye sahiptir. Bu nedenle, fizik derslerinde ve mühendislik uygulamalarında dolanma düzlemi kavramının derinlemesine incelenmesi esastır.
DOLANMA DÜZLEMİNİN KULLANIM ALANLARI
Dolanma düzlemi, çeşitli mühendislik ve bilim dallarında geniş bir kullanım alanına sahiptir. Mekanik sistemlerden astronotik çalışmalara, mühendislik bilgisayar modellemelerinden, biyomekanik araştırmalara kadar birçok alanda yer edinmiştir. Her bir alanda, dolanma düzleminin doğru bir şekilde belirlenmesi, yapılan çalışmaların doğruluğunu ve etkinliğini artırır.
DOLANMA DÜZLEMİ HESAPLAMALARINDA GEOMETRİK ANALİZ YÖNTEMLERİ
Dolanma Düzlemi hesaplamaları, karmaşık geometrik analiz yöntemleri gerektiren ve dikkatle ele alınması gereken bir konudur. Fizikte sıkça kullanılan bu hesaplamalar, çeşitli sorunları çözmeye yönelik önemli bilgileri açığa çıkarır. Dolanma düzlemi ile ilgili yapılacak çalışmaların başarısı için, uygulanan yöntemlerin doğru ve eksiksiz olması gerekmektedir. Bu bağlamda, geometrik analiz yöntemlerinin nasıl uygulandığını anlamak kritik bir önem taşır.
Geometrik Analiz Yöntemleri Adımları
- Veri toplama sürecinin başlatılması.
- Toplanan verilerin ön analizinin yapılması.
- Dolanma Düzlemi için gerekli parametrelerin belirlenmesi.
- Matematiksel modellerin oluşturulması.
- Analiz sonuçlarının yorumlanması.
- İhtiyaç duyulursa, model revizyonlarının gerçekleştirilmesi.
Bu adımlar, dolanma düzlemi hesaplamalarını düzgün bir şekilde gerçekleştirmek için izlendiğinde, daha doğru ve güvenilir sonuçlara ulaşılır. Böylelikle, yapılan analizlerin sağlam bir temele dayanması ve yanılma payının minimuma indirilmesi sağlanabilir. Aksi halde, küçük bir hata bile tüm hesaplamaların doğruluğunu tehlikeye atabilir. Bu nedenle, her bir adımın titizlikle ele alınması ve gözlemlenmesi gerekir.
TEMEL GEOMETRİK PRENSİPLER
Dolanma Düzlemi için temel geometrik prensiplerin bilinmesi, analiz yöntemlerinin doğru şekilde uygulanabilmesi açısından önem taşır. Geometrik analiz yöntemlerinde, doğrular, eğriler ve düzlemler arasındaki ilişkiler dikkatlice değerlendirilmelidir. Dürüst ve titiz bir analiz, başarıya giden yolda anahtardır. Bu prensipler ışığında, dolanma düzlemi hesaplamalarında daha anlamlı ve bilimsel sonuçlara ulaşılabilir.
HESAPLAMALAR İÇİN GEREKLİ VERİLER
Dolanma düzlemi hesaplamaları yapılırken, doğru ve güvenilir verilerin toplanması büyük öneme sahiptir. Veri toplama sürecinde belirli metotlar kullanılmalı ve bu veriler dikkatlice analiz edilmelidir. Eksik veya hatalı veriler, yanlış sonuçlara neden olabilir. Toplanan verilerin düzenli bir şekilde saklanması da hesaplama sürecindeki diğer önemli bir adımdır.
OLASI KARŞILAŞILAN SORUNLAR
Geometrik analiz sırasında dolanma düzlemi hesaplamalarında karşılaşabilecek sorunlar iyi bir ön hazırlık süreci ile minimize edilebilir. Yanlış verilerin kullanımı, algoritma hataları ya da gözden kaçan küçük detaylar hesaplamaların doğruluğunu etkileyebilir. Dolanma Düzlemi ile ilgili problemlerin çözümünde, detaylara dikkat etmek ve gerektiğinde profesyonel danışmanlıklardan yararlanmak önemlidir.




